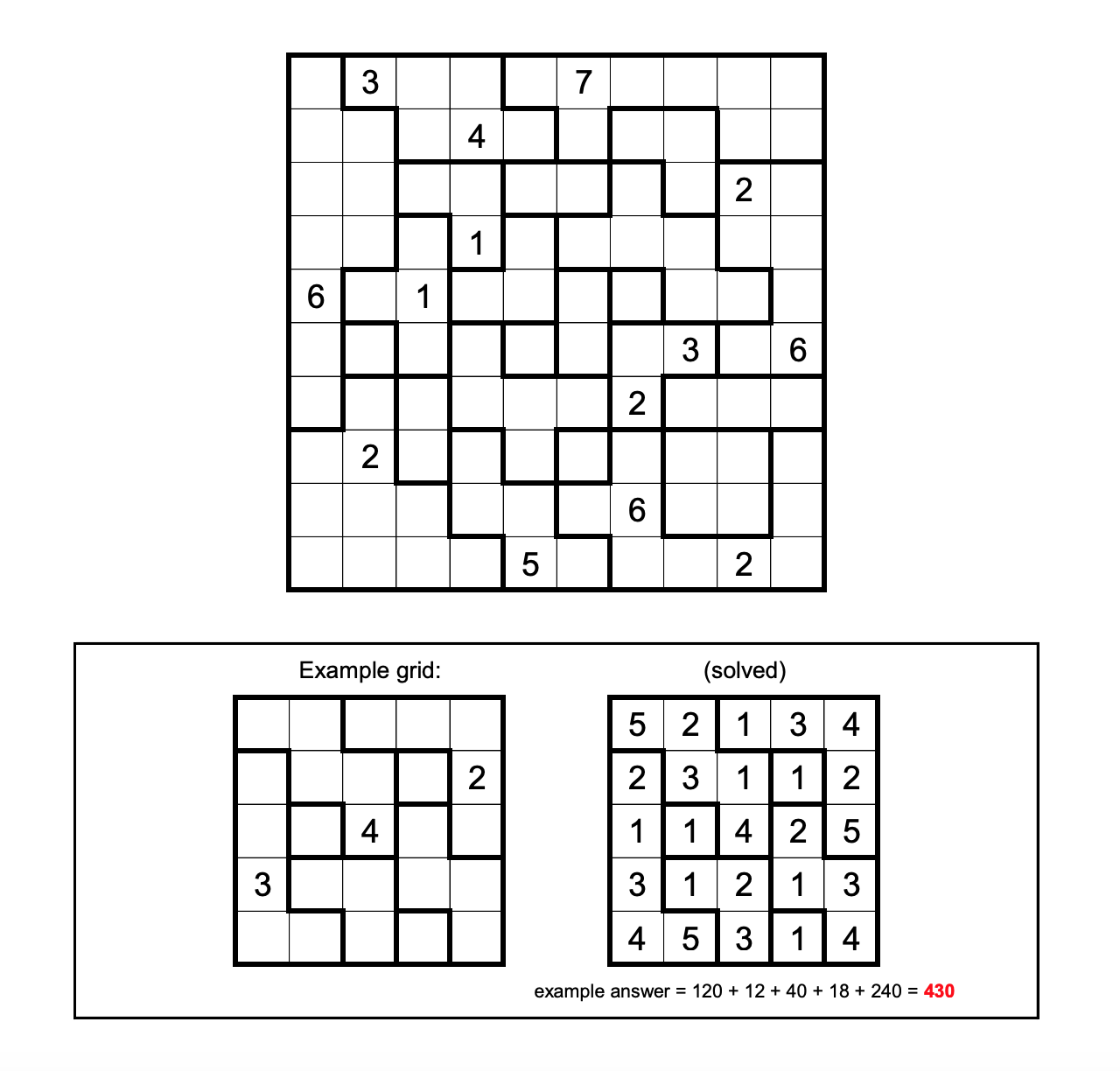
Jane Street Puzzle, June 2022: Block Party 4
In this month's Puzzle, we fill a grid using a SMT solver.
Fill each region with the numbers 1 through N, where N is the number of cells in the region. For each number K in the grid, the nearest K via taxicab distance must be exactly K cells away.
Once the grid is completed, the answer to the puzzle is found as follows: compute the product of the values in each row, and then take the sum of these products.
SMT Solver
We are going to use PySMT, a SMT solver API. I used the MathSAT5 solver as a backend, but PySMT is compatible with many solvers, including Z3.
from itertools import product
import numpy as np
from pysmt.shortcuts import And, Equals, Implies, Int, Not, Or, Solver, Symbol
from pysmt.typing import INT
region = np.array([
[0] + [1]*3 + [2]*6,
[0]*2 + [1]*3 + [2] + [3]*2 + [2]*2,
[0]*2 + [4]*2 + [5]*2 + [6, 3] + [7]*2,
[0]*2 + [8, 4, 9] + [6]*3 + [7]*2,
[0] + [8]*2 + [9]*2 + [10, 11] + [6]*2 + [7],
[0, 12, 8, 13, 14, 10] + [15]*2 + [7]*2,
[0, 16, 17] + [13]*3 + [15] + [20]*3,
[16]*2 + [17, 18, 13, 19, 22] + [21]*2 + [22],
[16]*3 + [18]*2 + [22]*2 + [21]*2 + [22],
[16]*4 + [18]*2 + [22]*4
])
region
Each cell is an integer variable:
R = range(10)
x = [[Symbol(f"{i},{j}", INT) for j in R] for i in R] # x[i][j] is the number row i, column j
f = True
for i, j in product(R, R):
f &= (1 <= x[i][j]) & (x[i][j] <= int((region == region[i][j]).sum()))
f
Two cells in the same region must be different:
def eq(i, j, k):
return Equals(x[i][j], Int(k))
def neq(i, j, k):
return Not(eq(i, j, k))
for i, j in product(R, R):
for i_, j_ in product(R, R):
if (i, j) < (i_, j_) and region[i][j] == region[i_][j_]:
f &= Not(Equals(x[i][j], x[i_][j_]))
For each cell with number $k$, the closest cell with number $k$ must be exactly $k$ cells away:
for i, j in product(R, R):
for k in range(1, region[i][j] + 1):
ok = [] # cells at distance k from (i, j)
nok = [] # cells at distance < k from (i, j)
for i_, j_ in product(R, R):
if abs(i - i_) + abs(j - j_) == k:
ok.append(eq(i_, j_, k))
if abs(i - i_) + abs(j - j_) < k and (i, j) != (i_, j_):
nok.append(neq(i_, j_, k))
f &= Implies(eq(i, j, k), And(Or(ok), And(nok)))
Initial values in the grid:
for (i, j, k) in [(0, 1, 3), (0, 5, 7), (1, 3, 4), (2, 8, 2), (3, 3, 1), (4, 0, 6), (4, 2, 1), (5, 7, 3), (5, 9, 6), (6, 6, 2), (7, 1, 2), (8, 6, 6), (9, 4, 5), (9, 8, 2)]:
f &= eq(i, j, k)
Finally, we can solve our problem:
with Solver() as solver:
solver.add_assertion(f)
if solver.solve():
V = [[solver.get_value(x[i][j]).constant_value() for j in R] for i in R]
for i in R:
for j in R:
print(V[i][j], "" if V[i][j] == 10 else " ", end=" ")
print()
The answer is the sum of the products of the values in each row:
from functools import reduce
from operator import mul
sum(reduce(mul, V[i]) for i in R)
Remark: this is not the only solution.

Comments