For the purposes of this puzzle, define a magic square to be a 3-by-3 grid of positive integers for which the rows, columns, and two diagonals all have the same sum.
An almost magic square is, well, almost a magic square. It differs from a magic square in that the 8 sums may differ from each other by at most 1.
For this puzzle, place distinct positive integers into the empty grid above such that each of four bold-outlined 3-by-3 regions is an almost magic square. Your goal is to do so in a way that minimizes the overall sum of the integers you use.

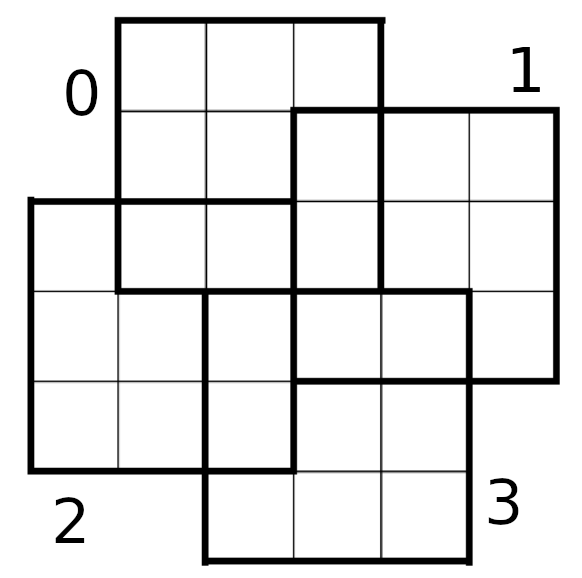
This problem can be solved by integer linear programming, using, for example, mip-python.
For each square $k$ (numbered from top to bottom) and for each $i, j$ coordinates, we define an integer variable $x_{i, j, k}$. Since there are overlaps between the squares, we equalize the variables in the same region:

from mip import *
import itertools

m, x = Model(), {}
for k, i, j in itertools.product(range(4), range(3), range(3)):
    if (i, j, k) in [(0, 0, 1), (1, 0, 1)]:
        x[i, j, k] = x[i + 1, 2, 0]
    elif (i, j, k) in [(0, 1, 2), (0, 2, 2)]:
        x[i, j, k] = x[2, j - 1, 0]
    elif (i, j, k) in [(0, 0, 3), (1, 0, 3)]:
        x[i, j, k] = x[i + 1, 2, 2]
    elif (i, j, k) in [(0, 1, 3), (0, 2, 3)]:
        x[i, j, k] = x[2, j - 1, 1]
    else:
        x[i, j, k] = m.add_var(var_type=mip.INTEGER, name=f"x{i}{j}{k}")
        m += x[i, j, k] >= 1

Then, we make sure that two variables $x, y$ refering to distinct cases are different. To do this, we introduce a binary variable $e$ with the following constraints: $$x \geq y + 1 - M\times e$$ $$y \geq x + 1 - M\times (1 - e)$$ With $M$ a big constant (considered as infinity). Depending on the value of $e$, these constraints reduce to:

• if $e = 0$: $x \geq y + 1$ (the other constraint $x \geq -\infty$ being useless)
• if $e = 1$: $y \geq x + 1$

Therefore those equations indeed ensure that $x, y$ are distinct.

e = {}

for i1, j1, k1 in itertools.product(range(3), range(3), range(4)):
    for i2, j2, k2 in itertools.product(range(3), range(3), range(k1 + 1)):
        if (i1, j1, k1) != (i2, j2, k2) and x[i1, j1, k1].name != x[i2, j2, k2].name:
            e[i1, j1, k1, i2, j2, k2] = m.add_var(var_type=mip.BINARY, name=f"e{i1}{j1}{k1}{i2}{j2}{k2}")
            m += x[i1, j1, k1] >= 1 + x[i2, j2, k2] - e[i1, j1, k1, i2, j2, k2]*150
            m += x[i2, j2, k2] >= 1 + x[i1, j1, k1] - (1 - e[i1, j1, k1, i2, j2, k2])*150

The "almost magic" property can be enforced by requiring every line, column and diagonal to have the same sum as the first line, $\pm$ 1:

def pm(c, l, e): # add constraint c = l +/- 1
    global m
    m += c <= l + e
    m += c >= l - (1 - e)

for k in range(4):
    e[k] = m.add_var(var_type=mip.BINARY, name=f"e{k}")
    l = x[0, 0, k] + x[0, 1, k] + x[0, 2, k] # first line
    for i in range(3):
        if i != 0:
            pm(x[i, 0, k] + x[i, 1, k] + x[i, 2, k], l, e[k])
        pm(x[0, i, k] + x[1, i, k] + x[2, i, k], l, e[k])
    pm(x[0, 0, k] + x[1, 1, k] + x[2, 2, k], l, e[k])
    pm(x[0, 2, k] + x[1, 1, k] + x[2, 0, k], l, e[k])

Let's check the size of the model:

print(f"Number of variables: {len(m.vars)}")
print(f"Number of constraints: {len(m.constrs)}")

Number of variables: 798
Number of constraints: 1616

Finally, let's optimize the sum:

m.objective = minimize(xsum(x[i, j, k] for i, j, k in itertools.product(range(3), range(3), range(4))))
m.verbose = 0
m.optimize(max_seconds=1200)

<OptimizationStatus.FEASIBLE: 3>

Here's the computed solution, for each square:

for k in range(4):
    for i in range(3):
        for j in range(3):
            print(f"{x[i, j, k].x}", end=" ")
        print()
    print()

print(f"Sum of integers: {m.objective_value}")

14 17 3 
1 11 22 
19 5 9 

22 40 8 
9 23 37 
39 7 24 

10 19 5 
6 12 16 
18 4 13 

16 39 7 
13 21 29 
34 2 26 

Sum of integers: 600.0

It turns out that this is an optimal solution, even though mip could not prove it in a reasonable time.